红黑树是具有着色性质的二叉查找树。平均红黑树和评级AVL树一样深,从而查找时间一般接近最优。同时红黑树执行插入操作时,产生的旋转相对较少,性能更优。
特性
- 每一个节点或者是红色,或者是黑色
- 根是黑色
- 如果一个节点是红色的,那么它的子节点必须是黑色的
- 任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等
- null节点为黑色
旋转
左旋
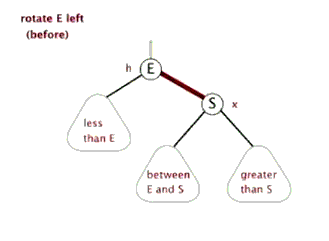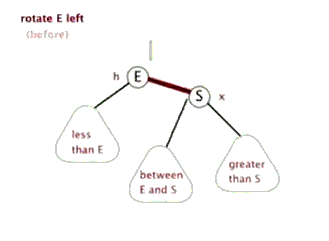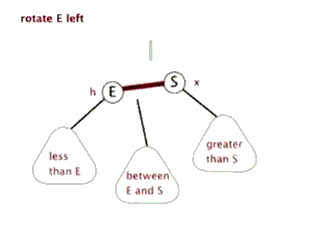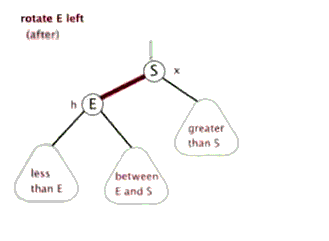
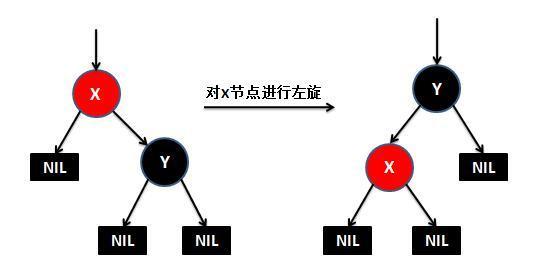
左旋做了三件事:
- 将y的左子节点赋给x的右子节点,并将x赋给y左子节点的父节点(y左子节点非空时)
- 将x的父节点p(非空时)赋给y的父节点,同时更新p的子节点为y(左或右)
- 将y的左子节点设为x,将x的父节点设为y
右旋
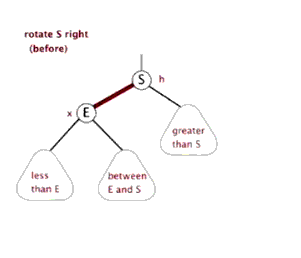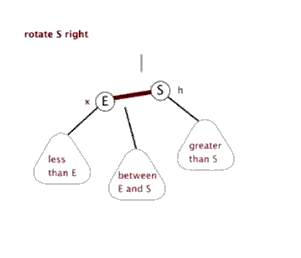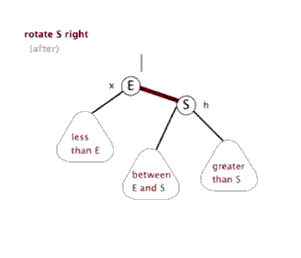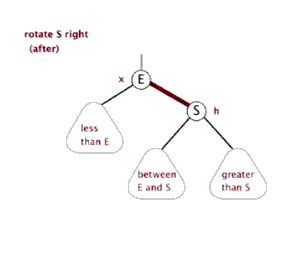
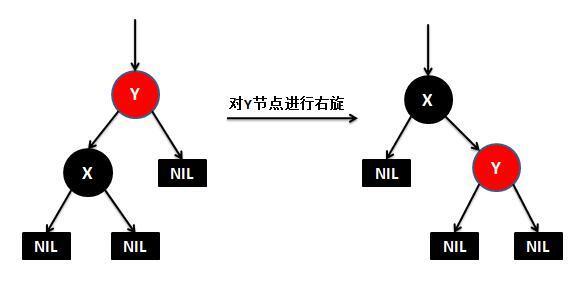
右旋做了三件事:
- 将x的右子节点赋给y的左子节点,并将y赋给x右子节点的父节点(x右子节点非空时)
- 将y的父节点p(非空时)赋给x的父节点,同时更新p的子节点为x(左或右)
- 将x的右子节点设为y,将y的父节点设为x
插入
首先,将红黑树当作一颗二叉查找树,将节点插入;然后,将节点着色为红色,这样就不会违背特性4;最后,通过旋转和重新着色等方法来修正该树,使之重新成为一颗红黑树。
新插入的节点分为三种情况:
- 新插入的节点是根节点,则直接着色为黑色
- 新插入的节点的父节点是黑色,则不需要做任何操作,就满足红黑树特性
- 新插入的节点的父节点是红色,则需要进行调整,使得结构满足红黑树特性,此时也有三种情况:
| 1 | 当前节点的父节点是红色,并且其叔叔节点也是红色 | 1、将父节点设为黑色;2、将叔叔节点设为黑色;3、将爷爷节点设为红色;4、将爷爷节点设为当前节点,继续操作 |
|---|---|---|
| 2 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点、父节点、爷爷节点成一字型 | 1、父节点设为黑色,爷爷节点设为红色;2、对爷爷节点进行单旋 |
| 3 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点、父节点、爷爷节点成之字型 | 1、将当前节点设为黑色,爷爷节点设为红色;2、对爷爷节点进行双旋 |
删除
删除操作会删除对应的节点,如果是叶子节点就直接删除,如果是非叶子节点,会用对应的中序遍历的后继节点来顶替要删除节点的位置。删除后就需要做删除修复操作,使的树符合红黑树的定义,符合定义的红黑树高度是平衡的。
红黑树的删除操作是最复杂的操作,复杂的地方就在于当删除了黑色节点的时候,如何从兄弟节点去借调节点,以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的,这样只能通过选择操作让他上升到父节点,而由于它是红节点,所以它的子节点就是黑的,可以借调。
对于兄弟节点是黑色节点的可以分成3种情况来处理,当所以的兄弟节点的子节点都是黑色节点时,可以直接将兄弟节点变红,这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的,需要往上追溯继续调整。
对于兄弟节点的子节点为左红右黑或者 (全部为红,右红左黑)这两种情况,可以先将前面的情况通过选择转换为后一种情况,在后一种情况下,因为兄弟节点为黑,兄弟节点的右节点为红,可以借调出两个节点出来做黑节点,这样就可以保证删除了黑节点,整棵树还是符合红黑树的定义的,因为黑色节点的个数没有改变。
红黑树的删除操作是遇到删除的节点为红色,或者追溯调整到了root节点,这时删除的修复操作完毕。